浮点运算是什么意思？

在计算机科学和数学计算领域，浮点运算是一种至关重要的数值计算方式。它能够处理大范围的实数，解决了整数运算无法精确表示小数和大数的局限，在科学计算、工程设计、金融分析等众多领域发挥着不可替代的作用。那到底什么是浮点运算呢？

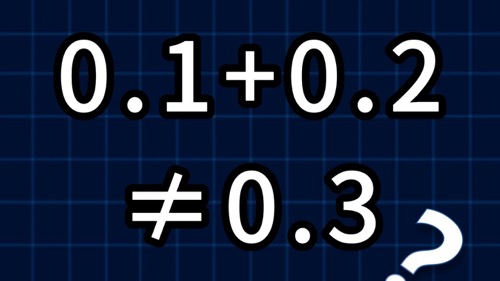
​一、浮点运算是什么意思？

浮点运算是指计算机处理带小数部分的数字时所进行的算术运算，包括加、减、乘、除等基本运算，以及更复杂的函数运算。​与整数运算不同，浮点数能够表示的数值范围更广，既可以表示非常大的数，也可以表示非常小的数。这就像我们在科学计数法中用a×10^b的形式表示数值一样，浮点运算通过类似的方式来高效地表示和处理实数。​

二、浮点数的构成是什么？​

从结构上看，一个浮点数通常由符号位、指数位和尾数位三部分组成，这一结构是基于IEEE754标准确定的。​

1、符号位：用于表示数值的正负，通常用1位二进制数表示，0表示正数，1表示负数。​

2、指数位：决定了浮点数的数量级，相当于科学计数法中的指数部分。指数位的位数越多，浮点数能够表示的范围就越大。​

3、尾数位：也称为有效数字位，用于表示数值的精度，相当于科学计数法中a的小数部分（通常a的整数部分为1，以保证表示的唯一性）。尾数位的位数越多，浮点数的精度就越高。​

三、浮点运算有什么特点？​

1、表示范围广：这是浮点运算最显著的特点。以32位单精度浮点数为例，它能够表示的数值范围大约在1.4×10^-45到3.4×10^38之间，而64位双精度浮点数的表示范围则更广阔，能满足绝大多数实际应用中对数值范围的需求。​

2、精度有限且存在误差：由于尾数位的位数是有限的，浮点运算无法精确表示所有的实数，会存在一定的舍入误差。例如，0.1这个简单的小数，在二进制浮点数表示中是一个无限循环小数，只能近似表示，多次运算后误差可能会累积，影响计算结果的准确性。​

3、运算复杂度高：相比整数运算，浮点运算的硬件实现和软件处理都更为复杂。整数运算的规则相对简单，而浮点运算需要考虑符号位、指数位和尾数位的协同处理，运算过程中还要进行对齐、舍入等操作，这使得浮点运算单元的设计难度更大，运算速度相对较慢。​